(c) means configurable using the config file
In the current version, there are no conception or birth events. Instead, the population size is kept constant by introducing a new person when somebody dies. The gender of the new person can be the same as the gender of the deceased person, or can be chosen based on a random number (c).
Executables
When the Simpact Cyan program is created, four executables are generated, each with its own properties as explained on the main page: simpact-cyan-basic-debug, simpact-cyan-basic, simpact-cyan-opt-debug and simpact-cyan-opt. The versions with 'basic' in the name use the straightforward implementation of the mNRM algorithm (which is very slow) while the 'opt' versions use the population-based algorithm. If 'debug' is specified in the filename the generated code includes debugging information (also slowing things down), otherwise faster code is generated which cannot be used by a debugger anymore.
Taking all this into account means that simpact-cyan-basic-debug is the slowest version and simpact-cyan-opt is the fastest. For a specific random number generator seed, they should all produce the same output though. By default, the seed is chosen at random, but for testing purposes a specific seed can be forced by setting the MNRM_DEBUG_SEED environment variable. On a Linux system for example, this can be done as follows:
On screen, you'd then see that the specified seed is being used:
This screen output is sent to stderr, the standard error stream. You can save this to a file by redirecting the output stream with identifier 2 to a file:
Saving this output somewhere is a good idea: in case you think something is wrong with the output you can not only run the other versions with the same seed to check that they produce the same result, but if something really is wrong you'll have a good starting point to start searching for the error. Similarly, even if you don't think there's something wrong with the output, it can be a good idea to run the four executables with the same seed from time to time. The only caveat is that you'll need to take into account the fact that the 'basic' versions are very slow, so it'll be necessary to limit the population size and the time that's simulated.
The last number on the command line in the previous examples was always 0. This indicates that the program should only make use of a single CPU core. If you set this to 1, a parallel version will be used that uses as many cores as OpenMP (the system used to calculate things using different CPU cores) allows. By default, this is as many cores as you have available on your computer, but this can be fixed to a specific amount by setting the OMP_NUM_THREADS environment variable. Note that specifying the parallel flag and setting OMP_NUM_THREADS=1 is not the same as specifying 0 as the parallel flag: the parallel version always activates certain safeguards to make sure that different cores don't modifiy the same piece of memory at the same time and this already slows things down.
Using all the cores instead of using a single core typically only causes a moderate speedup, and only when the population size is large enough. It can be helpful to see if the output for a larger simulation is plausible, but in case several runs are needed it's probably best to use the non-parallel version. For example, on a CPU with eight cores running eight non-parallel versions at the same time will be faster than running eight parallel versions, one after the other.
Input and output
Apart from the info about the executable version used and the seed used that is written to stderr, a number of output files will be created as well. Their names can be specified in a configuration file, which also contains various other parameters for the simulation.
The configuration file
The configuration file is a simple text file containing key-value pairs. Lines which start with the hash ('#') sign are ignored, allowing you to put comments in the configuration file. A fraction of a typical config file could look like this:
A sample config file is included in the source code and can be viewed here: config.txt. It contains many comments that should help clarify the different parameters. Note that in such a config file it's not possible to do calculations, not even simple ones. Therefore, instead of writing 1.0/2.0 as the value of some key, you'd need to write 0.5. Similarly, you can't write log(10), but need to write 2.30258509299404568401. Several config file parameters allow you to specify a certain 1D probability distribution. More information about the possible values can be found here: available 1D distributions.
Config file creator: configtool.py
Typically you'll want to use a specific configuration file for most of the settings, only wanting to change a few values. To make this possible, a simple Python program was written, called configtool.py. This program should be started with the Python interpreter as follows:
The defaultconfig.txt parameter is a normal config file as explained above. The file inputspec.csv is a CSV file that contains a description of which fields of the default config file should be modified and what values they should take. The program will create a number of new configuration files, based on the default file and the specified modifications, and will generate a number of output files, as many as there are lines with values in the CSV file. All these output files will start with outputprefix, the exact names will depend on what's specified in the inputspec.csv file.
The general format of the CSV file is as follows:
By default, the output file name will consist of the output prefix, followed by the row number in the CSV file, followed by ".txt". If the first field name is "Scenario ID" however, instead of using the row number the corresponding identifier is used for the output file. For example if the config file looks like this:
and the outputprefix parameter is Out_, then the following files will be generated:
- Out_scen_1.txt
- Out_scen_2.txt
- ...
There are a few special values that you can specify in such a CSV file:
*means that the value from the default config file should not be changed in the generated config file%IDmeans that the identifier for the scenario (either from the 'Scenario ID' column, or from the row number) should be substituted.
A small example for such a CSV file could then look as follows:
The log files
In the configuration file there are three fields that specify additional log files:
- logsystem.filename.events: in this log file, the events that take place are written
- logsystem.filename.persons: this is a log file containing the information about the people in the simulation
- logsystem.filename.relations: logs the relationships between people in the simulation
Event log
In the event log file there are at least 10 fields, containing the following information:
- Event time
- Event name
- Person 1 name
- Person 1 ID
- Person 1 gender (0 = man, 1 = woman)
- Person 1 age
- Person 2 name
- Person 2 ID
- Person 2 gender (0 = man, 1 = woman)
- Person 2 age
For events that don't involve two persons, the person ID is set to -1 and the name to "(none)". Some example lines could look as follows:
After these ten fields, depending on the event type, additional fields may follow. In that case, a description of the field preceeds the actual value. For example:
Some event names are between parentheses, e.g. "(relationshipended)". That means that it was not a real event in the mNRM system, but rather something triggered by an event. For example the "(relationshipended)" pseudo-event is triggered by both a dissolution event and mortality events. For example:
In this example you can see a real 'normalmortality' event, which triggers two 'relationshipended' pseudo-events as well as a 'newperson' pseudo-event. In this case, the death of a person means that the relationships he was in need to be dissolved; to keep the population size constant a new person is introduced as well.
Person log
The person log file currently contains thirteen fields:
ID: Person ID (integer starting with 0)Gender: Gender: 0 = man, 1 = womanTOB: time of birthTOD: time of deathIDF: Father IDIDM: Mother IDTODebut: debut timeFormEag: formation eagernessInfectTime: infection timeInfectOrigID: infection origin IDInfectType: infection type: -1 = not infected, 0 = seed, 1 = sexual transmission, 2 = MTCTlog10SPVL: base 10 logarithm of the set-point viral loadTreatTime: treatment time
Relationship log
The relationship log contains five fields describing the relationships that occurred during the simulation.
IDm: ID of manIDw: ID of womanFormTime: formation timeDisTime: dissolution timeAgeGap: age man - age woman
Initial population and initial events
The population is initialized with a number of men and a number of women, for a total initial population size of N_start people. Their initial ages are drawn from a distribution based on a CSV file (c), and if the initial age is older than the debut age (c), the person is marked a 'sexually active'. For people who are not sexually active yet, a 'debut' event is scheduled. Each person also has an initial 'mortality event' scheduled.
If seeding of the HIV infection is enabled (c), a global 'HIV seeding' event is scheduled. When that event fires, a specific fraction (c) of the population will be marked as being infected with HIV.
Event overview
AIDS mortality event
When a person becomes infected at a certain time 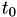 , an AIDS mortality event is scheduled. The survival time is calculated as
, an AIDS mortality event is scheduled. The survival time is calculated as
![\[ t_{surv} = \frac{C}{V_{sp}^{-k}} \]](form_114.png)
so the event is scheduled to fire at 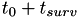 . When the person receives treatment, this causes a drop in
. When the person receives treatment, this causes a drop in 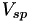 and the event fire time is adjusted to that it fires at
and the event fire time is adjusted to that it fires at 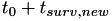 . The constants C and k can be configured in the configuration file (c).
. The constants C and k can be configured in the configuration file (c).
When the event fires, the affected relationships are dissolved. To keep the population size constant, a new person is introduced into the population, the gender of whom can be either the same as the gender of the deceased person or can be chosen randomly (c).
Details
To accomplish this without having to cancel the existing AIDS mortality event, a hazard-like scheme is used. When the event originally gets scheduled, 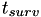 is calculated and a factor
is calculated and a factor 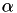 is set to
is set to 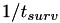 . The internal time interval until the event fires is just set to 1, and internal time intervals
. The internal time interval until the event fires is just set to 1, and internal time intervals 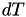 are mapped onto real-world time intervals
are mapped onto real-world time intervals 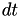 using
using 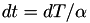 . This way, when the internal time interval of 1 would pass, a real world time interval of
. This way, when the internal time interval of 1 would pass, a real world time interval of 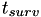 would have passed.
would have passed.
The treatment of a person needs to affect the real world time at which this event is fired. To do so, the factor alpha is calculated to be a different value when a person is receiving treatment. The change is such that the event now fires at real world time 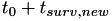 .
.
Mortality event
A regular mortality event is always present for every person, and represents a non-AIDS cause of death. The fire time for this event is based on a Weibull distribution, taking into account a gender based difference (c). This is just a fixed event fire time.
When the event fires, the affected relationships are dissolved. To keep the population size constant, a new person is introduced into the population, the gender of whom can be either the same as the gender of the deceased person or can be chosen randomly (c).
Chronic stage event
To mark the transition from the acute stage of HIV infection to the chronic stage, this event is used. The event is currently set to fire after a fixed amount of time, configurable using the config file (c). When the event fires, the person is simply marked as being in the chronic stage.
Debut event
When this event fires, the relevant person is marked as being sexually active. Because at this point relationships with other people become possible, relationship formation events are scheduled for this person and every sexually active person of the opposite sex. This event is currenly set to take place when the person becomes 15 years old, but is configurable using the config file (c).
Formation event
There are currently two types of formation events: a 'simple' formation event and an 'agegap' formation event (c), each using its own hazard. A formation event is a more typical MNRM event: the internal time is picked from a simple exponential distribution and is mapped onto a real world time using a hazard function.
Each of the versions has a t_max config line, which is a measure for when the hazard becomes constant. More precisely, the hazard will become constant after
![\[ min(t_{b,1}, t_{b,2}) + t_{max} \]](form_121.png)
where 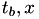 is the date of birth of a person in the relationship. By using this
is the date of birth of a person in the relationship. By using this t_max parameter, the necessary calculations become possible and if the value is larger than the typical lifetime of a person it will yield the expected results.
When the formation event fires, some bookkeeping is done to keep track of the relationships between persons, and a dissolution event for the same people is scheduled. If precisely one of the persons is infected, a HIV transmission event is scheduled for transmission from one person to the other.
'Simple' formation event
In this case, the hazard is of the form
![\[ h = \exp\left(a_{0,total} + a_1 P_i + a_2 P_j + a_3 |P_i - P_j| +a_4 \frac{A_i+A_j}{2} + a_5 |A_i-A_j-D_p| + b t_{diff}\right) \]](form_123.png)
The 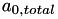 value is calculated as follows:
value is calculated as follows:
![\[ a_{0,total} = a_0 + a_6 (e_i + e_j) + a_7 |e_i - e_j| - \textrm{ln}\left(\frac{N_{start}}{2}\right) \]](form_125.png)
In this last term, the initial population size 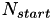 is taken into account. The
is taken into account. The 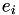 and
and 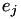 are 'eagerness' parameters for the persons involved. All these hazard parameters can be configured in the config file (c).
are 'eagerness' parameters for the persons involved. All these hazard parameters can be configured in the config file (c).
Calculations for this hazard can be found here: formationhazard.pdf
'Agegap' formation event
For the newer 'agegap' formation hazard, the hazard is of the form:
![\[ \begin{array}{ll} h = \exp\left(\right. & a_{0,total} + a_{numrel,man} P_i + a_{numrel,woman} P_j \\ & + a_{numrel,diff} |P_i-P_j| + a_{meanage} \frac{A_i+A_j}{2} \\ & + a_{gap,factor,man} | A_i - A_j - D_{p,i} - a_{gap,agescale,man} A_i | \\ & + a_{gap,factor,woman} | A_i - A_j - D_{p,j} - a_{gap,agescale,woman} A_j | \\ & \left. + b t_{diff} \right) \end{array} \]](form_129.png)
Here, 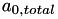 value is calculated as follows:
value is calculated as follows:
![\[ a_{0,total} = a_{baseline} + a_{eagerness,sum} (e_i + e_j) + a_{eagerness,diff} |e_i - e_j| - \textrm{ln}\left(\frac{N_{start}}{2}\right) \]](form_130.png)
In this last term, the initial population size 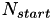 is taken into account. The
is taken into account. The 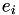 and
and 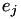 are 'eagerness' parameters for the persons involved. The
are 'eagerness' parameters for the persons involved. The 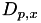 values are the preferred age differences which are defined on a per-person basis in this case. All these hazard parameters can be configured in the config file (c).
values are the preferred age differences which are defined on a per-person basis in this case. All these hazard parameters can be configured in the config file (c).
Calculations for this hazard can be found here: formationhazard_agegap.pdf
Dissolution event
A relationship dissolution event is very similar to the 'simple' relationship formation event, with a very similar hazard. In this case however, the a_0,total term is just a constant a_0 from the config file (c), and the initial population size N_start is not taken into account. As with the formation event, a parameter t_max is used to make it possible to work with the exponential hazard.
The only actions that happen when a dissolution event fires, is that the recorded relationship between the two people is removed and that a new formation event between the same people is scheduled.
HIV 'seeding' event
The start of the HIV epidemic is triggered by this global event. The time at which it fires can be defined in the configuration file and will only take place if that time is positive. For a negative time, HIV will not be introduced into the population.
When this event fires, a specific fraction (c) of the population will be marked as HIV infected. For those infected, an AIDS based mortality event will be scheduled as well as a 'chronic stage event'. If treatment is enabled (c), a treatment event will be scheduled for the infected person as well. The existing relationships are checked as well: if a person is infected and his/her partner is not, a transmission event will be scheduled.
Transmission event
A transmission event contains references to two people, the origin of the infection and the person that will be infected. The event gets cancelled when this second person already became infected, or when the relationship between the two people was dissolved.
This is again a regular MNRM event, with an internal time picked from an exponential distribution. The mapping onto a real world time is done using the hazard
![\[ h = \exp\left(a + b V^{-c} \right) \]](form_132.png)
in which V is the current viral load, and the other constants are read from the config file (c). The viral load V can be the set-point viral load in the chronic stage, or a higher one in the acute stage. In the acute stage, the viral load is calculated from the set-point viral load 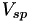 using the formula
using the formula
![\[ V = \left[ \max\left(\frac{\textrm{ln}(x)}{b} + V_{sp}^{-c}, \textrm{maxvalue}^{-c}\right) \right]^{-\frac{1}{c}} \]](form_133.png)
for 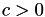 or with a
or with a min function otherwise. Here, 'x' (c) is currently set to 10 and b and c are the same parameters from before.
When the event fires, the second person is also marked as being infected with the first person as the origin. A 'chronic stage event' will be scheduled to mark the transition from acute to chronic stage, an AIDS based mortality event will be scheduled as well as a treatment event. For every relationship the newly infected person is in, if the other person is not infected a transmission event will be scheduled.
Treatment event
In this simulation, when a person becomes infected a treatment event is scheduled if treatment is enabled in the config file. The fire time for this event is based on the set-point viral load: calling
![\[ t_{surv} = \frac{C}{V_{sp}^{-k}} \]](form_114.png)
the time until the event fires is
![\[ t_{surv} f_1 \]](form_135.png)
Here, 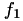 is a fixed fraction (c) of the expected survival time which will pass until the person receives treatment.
is a fixed fraction (c) of the expected survival time which will pass until the person receives treatment.
When the event fires, the set-point viral load of the person in question is lowered. Since the acute stage viral load is always calculated from the set-point viral load, this also causes the acute stage viral load to be lowered.
Lowering the set-point viral load is done using a fraction 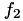 (c) on a logarithmic scale:
(c) on a logarithmic scale:
![\[ \textrm{ln}\left(V_{sp,new}\right) = \textrm{ln}\left( V_{sp} \right) f_2 \Leftrightarrow V_{sp,new} = V_{sp}^{f_2} \]](form_138.png)
Person
A person stores bookkeeping data, such as which relationships he/she is is, whether the person is infected or not etc. The relationship formation 'eagerness' parameter e_i for this person is picked from a distribution of which the type and parameters are configurable (c). When a person is marked as being infected, the set-point viral load is also determined and this procedure depends on the type of infection and the settings in the configuration file. The model type can be either 'logweibullwithnoise' or 'logbinormal'.
'logweibullwithnoise'
If the person is an infection 'seed', i.e. a person marked as infected at the start of the simulation, the set-point viral load is based on a Weibull distribution (c):
![\[ \log_{10}\left(V_{sp}\right) = \textrm{pickWeibullNumber}(\textrm{scale},\textrm{shape}) \]](form_139.png)
If another person is the origin, that person's viral load is inherited and some randomness is added:
![\[ V_{sp} = \textrm{pickGaussianNumber}\left(V_{sp,origin}, \sigma\right) \]](form_140.png)
For simplicity, the sigma parameter is set to a specific fraction (c) of Vsp,origin. If this procedure would yield a negative number, a new Vsp value is chosen using the same procedure or based on the Weibull distibution (c).
'logbinormal'
In this case, both the initial 'seed' value and the inherited 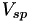 value are chosen so that the 2D distribution
value are chosen so that the 2D distribution 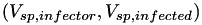 is a clipped binormal distribution (on a log scale). The shape parameters (mean, sigma), clipping parameters (min, max) and the correlation parameter (rho) are all configurable in the config file.
is a clipped binormal distribution (on a log scale). The shape parameters (mean, sigma), clipping parameters (min, max) and the correlation parameter (rho) are all configurable in the config file.
 1.8.6
1.8.6