Introduction
Simpact Cyan is an event driven simulation framework intended for the study of HIV infection spread in South Africa. The core event based framework is reusable in other contexts as well and does not contain any specific reference to HIV or South Africa. Instead, a very general set of classes is provided which are intended to be used for population-based simulations. This means that for the most part, the state of a simulation consists of the people in the population and events in the simulation will affect those people.
As will be explained below, the algorithm used is called the modified Next Reaction Method and is not specific to population based simulations. Another very trivial implementation is provided as well, apart from the population-based implementation, but this is in no way optimized and will perform poorly. But because it is such a straightforward implementation, it can provide a good reference simulation to compare the more optimized version to.
Event based simulations
Internal times and real world times
In the event based framework we'll be using, event times are based on an internal clock 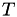 . These event times are generated at random: the first random number
. These event times are generated at random: the first random number 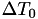 determines an internal event fire time
determines an internal event fire time 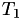 . Then, a new random number
. Then, a new random number 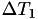 is generated telling the algorithm that the next internal event time is
is generated telling the algorithm that the next internal event time is
![\[ T_2 = T_1 + \Delta T_1 \]](form_37.png)
The situation is illustrated in the figure below, where in general
![\[ T_{i+1} = T_i + \Delta T_i \]](form_38.png)
Typically, the random numbers 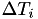 will be chosen from an exponential distribution, but in principle this could be different.
will be chosen from an exponential distribution, but in principle this could be different.

This simple time line of the internal clock is subsequently mapped onto real world times 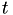 using a propensity function or hazard
using a propensity function or hazard 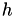 , using the following integral equation:
, using the following integral equation:
![\[ T = \int_0^t h(s) ds \]](form_42.png)
Since the 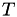 values are the ones that are known, this integral equation must be solved for
values are the ones that are known, this integral equation must be solved for 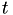 to calculate the corresponding real world time. This mapping can be simply a speedup or slowdown of time, or could be something more complicated, as hinted at by the figure below.
to calculate the corresponding real world time. This mapping can be simply a speedup or slowdown of time, or could be something more complicated, as hinted at by the figure below.
If we write the equation above for a general 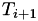 , we get:
, we get:
![\[ T_{i+1} = \int_0^{t_{i+1}} h(s) ds = \int_0^{t_i} h(s) ds + \int_{t_i}^{t_{i+1}} h(s) ds \]](form_44.png)
![\[ \Leftrightarrow T_{i+1} = T_i + \int_{t_i}^{t_{i+1}} h(s) ds \]](form_45.png)
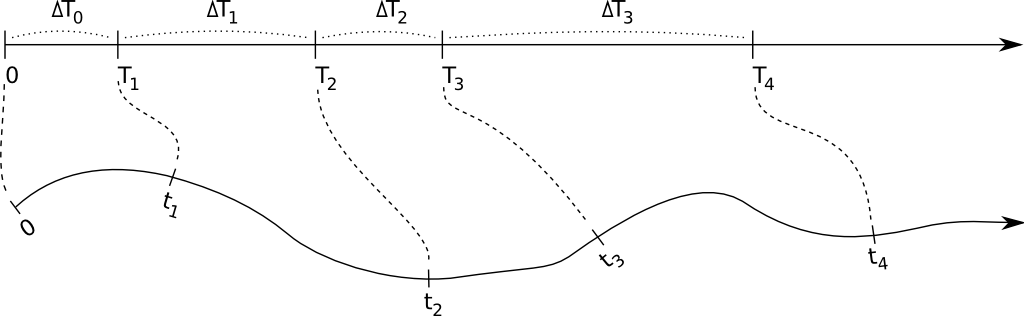
![\[ \Leftrightarrow T_{i+1} - T_i = \Delta T_i = \int_{t_i}^{t_{i+1}} h(s) ds \]](form_46.png)
So if the real world event fire time 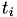 is known, the generated random number
is known, the generated random number 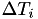 determines the next real world event time
determines the next real world event time 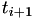 by solving the integral equation
by solving the integral equation
![\[ \Delta T_i = \int_{t_i}^{t_{i+1}} h(s) ds \]](form_49.png)
Multiple event types and simulation state
We'll be working with some kind of simulation state 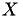 that changes during the simulation, but only changes when an event is fired: in between events the simulation state does not change. So for example
that changes during the simulation, but only changes when an event is fired: in between events the simulation state does not change. So for example
![\[ X(t) = X(t_i) {\rm \ if\ } t \in [t_i,t_{i+1}[ \]](form_51.png)
A hazard can be time dependent both because it depends on the simulation state, and because there is some intrinsic time dependence. The relationship between internal times and real world times then becomes
![\[ \Delta T_i = \int_{t_i}^{t_{i+1}} h(X(s),s) ds = \int_{t_i}^{t_{i+1}} h(X(t_i),s) ds \]](form_52.png)
where we used the fact that the simulation state is constant in between events.
In a general simulation there will be more than one event type, each having its own internal time line. These internal time lines do not influence each other, but because an event can change the simulation state, the mapping through the hazard function onto real world times can become different in one time line because of an event generated in another time line.
Suppose for a specific internal time line, at one point we've generated the random number 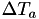 which is mapped onto a next real world event time
which is mapped onto a next real world event time 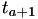 through the equation
through the equation
![\[ \Delta T_a = \int_{t_a}^{t_{a+1}} h(X(s),s) ds = \int_{t_a}^{t_{a+1}} h(X(t_a),s) ds \]](form_55.png)
where in the last equality we've used the fact that we're assuming the state won't change in 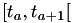 .
.
That's all it is of course, an assumption, because events from another time line could very well fire during that interval and change the state. Suppose that this is the case, that because of some other timeline another event changed the state at time 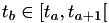 . This implies that the last equality in the previous equation is no longer valid; instead, the equation becomes:
. This implies that the last equality in the previous equation is no longer valid; instead, the equation becomes:
![\[ \Delta T_a = \int_{t_a}^{t_{a+1}} h(X(s),s) ds = \int_{t_a}^{t_b} h(X(t_a),s) ds + \int_{t_b}^{t_{a+1}} h(X(t_b),s) ds \]](form_58.png)
Here we've used the fact that we now know that 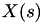 remained constant in
remained constant in 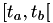 and that we're re-calculating the next fire time
and that we're re-calculating the next fire time 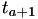 based on the assumption that the state will remain constant in
based on the assumption that the state will remain constant in 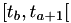 .
.
To calculate the next scheduled event fire time 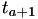 , we first subtract the internal time interval corresponding to
, we first subtract the internal time interval corresponding to 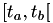 from
from 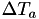 , let's call the result
, let's call the result 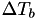 :
:
![\[ \Delta T_b \equiv \Delta T_a - \int_{t_a}^{t_b} h(X(t_a),s) ds \]](form_64.png)
Then, we need to solve for 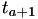 using the following equation
using the following equation
![\[ \Delta T_b = \int_{t_b}^{t_{a+1}} h(X(t_b),s) ds \]](form_65.png)
which is very similar to the equation for our first calculation for 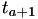 , but now starting from
, but now starting from 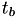 and using the adjusted internal time
and using the adjusted internal time 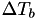 .
.
Note that if the hazard is not explicitly time dependent, the fact that the simulation state does not change in between event fire times, really speeds up the procedure since the integral becomes trivial:
![\[ \int_{t_a}^{t_{a+1}} h(X(s)) ds = \int_{t_a}^{t_{a+1}} h(X(t_a)) ds = h(X(t_a)) \int_{t_a}^{t_{a+1}} ds = (t_{a+1}-t_a) h(X(t_a)) \]](form_67.png)
Modified next reaction method
Core algorithm
This procedure, predicting the next real world event fire time and correcting it if another event fires first, is the basis of the modified Next Reaction Method (mNRM). Suppose there are 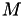 event types, each with their own internal time line and call
event types, each with their own internal time line and call 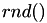 a function that returns a random number in
a function that returns a random number in ![$[0,1]$](form_70.png) (uniform). The modified Next Reaction Method, where internal time intervals are picked from an exponential distribution
(uniform). The modified Next Reaction Method, where internal time intervals are picked from an exponential distribution 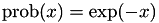 , then works as follows:
, then works as follows:
- Initialization:
- for
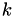 from
from 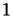 to
to 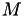 ,
, 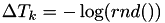
This picks numbers from an exponential distribution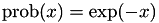 and correspond to the initial internal fire times for the different event types (which still need to be mapped onto real world times using the hazards). Note that here the index
and correspond to the initial internal fire times for the different event types (which still need to be mapped onto real world times using the hazards). Note that here the index 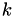 refers to a specific timeline whereas above it referred to time differences within the same timeline.
refers to a specific timeline whereas above it referred to time differences within the same timeline. - set
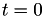
- for
- Loop:
- for
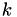 from
from 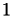 to
to 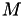 , calculate
, calculate 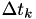 so that
so that 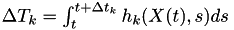
This translates the time left from the exponential distribution into a physical time that should pass until the event fires. - call
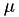 the index for which
the index for which 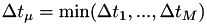
This is the event type that shall fire first. - for
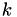 from
from 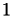 to
to 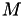 except
except 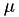 , change
, change 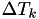 to
to 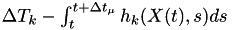
Note that because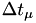 is the smallest of them all, the integral will be smaller than the one in 1., and
is the smallest of them all, the integral will be smaller than the one in 1., and 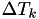 will stay positive (unless there's some really strange hazard, which of course should not happen)
will stay positive (unless there's some really strange hazard, which of course should not happen) - add
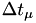 to
to 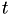
- fire event
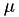 which can change the simulation state
which can change the simulation state - set
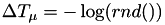
For this particular event, no next internal time is available yet, so we need to pick a new internal time from an exponential distribution.
- for
Optimizations
It may not be necessary to do the 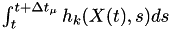 calculation every time. If the state changes due to each event, and this influences all hazard functions, then we really do need to calculate every
calculation every time. If the state changes due to each event, and this influences all hazard functions, then we really do need to calculate every
![\[ \Delta T_{k,1} = \int_{t_1}^{t_2} h_k(X(t_1),s) ds \textrm{, } \Delta T_{k,2} = \int_{t_2}^{t_3} h_k(X(t_2),s) ds \textrm{, } \Delta T_{k,3} = \int_{t_3}^{t_4} h_k(X(t_3),s) ds \textrm{, etc.} \]](form_87.png)
However, if the hazard does not change for a particular time line 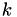 , then instead of calculating each
, then instead of calculating each 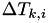 above, we can save some unnecessary recalculations by just calculating an integral
above, we can save some unnecessary recalculations by just calculating an integral
![\[ \Delta T_{k,sum} = \int_{t_0}^{t_{end}} h_k(X(t_0),s) ds \]](form_89.png)
Where in the core mNRM each event time line only needs to keep track of it's own internal 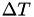 value (because the mapping to the real world time is calculated over and over again), to make this new approach work some additional bookkeeping is needed to keep track of when the events would fire in real time.
value (because the mapping to the real world time is calculated over and over again), to make this new approach work some additional bookkeeping is needed to keep track of when the events would fire in real time.
- Initialization:
- for
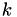 from
from 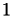 to
to 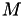 ,
, 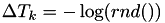
This picks numbers from an exponential distribution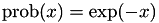
- set
- for each
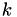 , we must also know the time at which this calculation of
, we must also know the time at which this calculation of  took place. For now this is just
took place. For now this is just 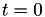 , so we set
, so we set 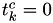 for all
for all  .
. - for each
 , map these internal Poisson intervals
, map these internal Poisson intervals 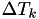 to event fire times
to event fire times 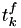 using the hazards:
using the hazards: ![\[ \Delta T_k = \int_{t^c_k}^{t^f_k} h_k(X(t^c_k),s) ds \]](form_94.png)
- for
- Loop:
- for
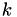 from
from 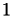 to
to 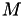 , calculate the minimum real time that would elapse until an event fires:
, calculate the minimum real time that would elapse until an event fires: 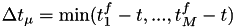 . Here
. Here 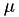 is the index of the event that corresponds to this minimal value.
is the index of the event that corresponds to this minimal value. - add
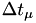 to
to 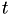
- only for the event types
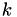 for which the hazards will be affected by
for which the hazards will be affected by 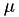 , we need to do the following:
, we need to do the following:- Diminish the internal time
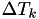 with the internal time that has passed:
with the internal time that has passed:
Here![\[ \Delta T_k := \Delta T_k - \int_{t^c_k}^{t} h_k(X(t^c_k),s) ds \]](form_96.png)
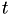 is the new time, and the hazards are still the old hazard!
is the new time, and the hazards are still the old hazard! - Set
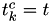 , i.e. store the time at which this
, i.e. store the time at which this 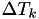 was calculated.
was calculated.
- Diminish the internal time
- fire event
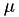 (changing the state), pick a new
(changing the state), pick a new 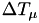 value from the exponential distribution, set
value from the exponential distribution, set 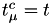 and calculate
and calculate 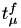 accordingly.
accordingly. - only for the events
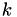 for which the hazards were affected by
for which the hazards were affected by 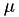 , we need to recalculate the real fire times of these events: calculate
, we need to recalculate the real fire times of these events: calculate 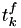 so that this holds:
so that this holds:
Note that![\[\Delta T_k = \int_{t^c_k}^{t^f_k} h_k(X(t^c_k),s) ds \]](form_102.png)
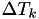 and
and 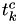 were adjusted in step 3, so we're using the new hazards.
were adjusted in step 3, so we're using the new hazards.
- for
If one keeps track of which event affects which, this can really save some calculation time. It's also possible to determine more efficiently which event will fire next, not needing to inspect all scheduled event fire times at every loop.
A slightly re-ordered version (for positive times only since we use a negative one as a marker), which is nearly identical to the one used in the program code is the following:
- Initialization:
- set
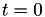
- for
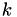 from
from 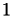 to
to 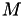 , let
, let 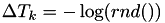 . Set
. Set 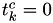 and set
and set 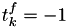 to indicate that this event time still needs to be calculated from the
to indicate that this event time still needs to be calculated from the 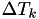 version.
version.
- set
- Loop:
- for
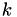 from
from 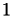 to
to 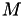 , if
, if 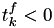 then calculate
then calculate 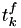 from the stored
from the stored 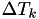 value so that:
value so that: ![\[\Delta T_k = \int_{t^c_k}^{t^f_k} h_k(X(t^c_k),s) ds \]](form_102.png)
- for
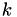 from
from 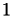 to
to 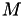 , calculate the minimum real time that would elapse until an event takes place:
, calculate the minimum real time that would elapse until an event takes place: 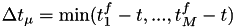 . Here
. Here 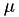 is the index of the event that corresponds to this minimal value.
is the index of the event that corresponds to this minimal value. - only for the events
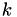 for which the hazards will be affected by
for which the hazards will be affected by 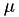 , we need to do the following:
, we need to do the following:- Diminish the internal time
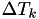 with the internal time that will have passed when
with the internal time that will have passed when 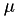 fires:
fires:
Here![\[ \Delta T_k := \Delta T_k - \int_{t^c_k}^{t + \Delta t_\mu} h_k(X(t^c_k),s) ds \]](form_107.png)
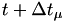 is the fire time, and the hazards are still the old ones!
is the fire time, and the hazards are still the old ones! - Set
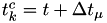 and set
and set 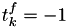 to indicate that it still needs to be calculated from the remaining
to indicate that it still needs to be calculated from the remaining 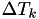 .
.
- Diminish the internal time
- add
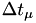 to
to 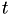
- fire event
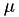 (changing the state), generate a new
(changing the state), generate a new 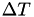 value, set
value, set 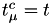 and set
and set 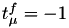 to indicate that
to indicate that 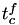 should be calculated from
should be calculated from 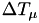 .
.
- for
Implementation of mNRM
While in the outline above there are a fixed number of 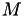 event types, this does not need to be the case. Event types could be added or removed dynamically without any problem. In the case of the population based simulations in this project, we will just talk about a number of events in which each event only fires once and is then discarded. This corresponds to the situation where there are as many time lines as events, being added and destroyed dynamically, but since each 'time line' will only use a single internal time interval it's not really a line anymore.
event types, this does not need to be the case. Event types could be added or removed dynamically without any problem. In the case of the population based simulations in this project, we will just talk about a number of events in which each event only fires once and is then discarded. This corresponds to the situation where there are as many time lines as events, being added and destroyed dynamically, but since each 'time line' will only use a single internal time interval it's not really a line anymore.
Basic algorithm implementation
The last algorithm presented above fits in the abstraction used by the State class, in the State::evolve function:
A very straightforward implementation of the necessary functions can be found in the SimpleState class. Like in the very basic mNRM algorithm, for each event executed, all other event times are always recalculated. This makes the procedure very slow of course, but it is a good reference to test a more advanced implementation against.
To create a simulation with this version of the algorithm, you need to provide implementations for the SimpleState::getCurrentEvents and SimpleState::onFiredEvent functions. The first function must return a list of all events in the system, the second one can modify the list of events, for example removing the event that just fired if no longer needed.
The code that implements initEventTimes looks as follow:
The code for the getNextScheduledEvent implementation looks as follows:
Here, the key calculation is the solveForRealTimeInterval one, which solves for 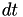 in the integral
in the integral
![\[ \Delta T = \int_{\rm curTime }^{{\rm curTime} + dt} h(X({\rm curTime}),s) ds \]](form_15.png)
where 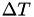 is the current (remaining) internal time interval for an event.
is the current (remaining) internal time interval for an event.
Finally, the advanceEventTimes implementation is the following:
Here, the internal time 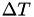 for an event is replaced by
for an event is replaced by
![\[ \Delta T - \int_{t^c}^{t_1} h(X(t^c),s) ds \]](form_16.png)
where 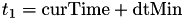 and
and 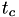 is the time at which the mapping between internal time interval and real world fire time was last calculated.
is the time at which the mapping between internal time interval and real world fire time was last calculated.
Population based algorithm
As was said before, the previous implementation from SimpleState is slow as in general it will perform a large amount of unnecessary recalculations. For this reason, for the Simpact Cyan project, a population-based implementation of the mNRM was created as well. The core of this algorithm is provided by the Population class, which defines the population as a set of people represented by a PersonBase class and which fires events derived from PopulationEvent.
These classes simply perform the core functions to make the mNRM work, but are intended to be extended. For this reason, the Simpact Cyan project defines a number of classes based on those:
- Person, Man and Woman: The Person class is derived from PersonBase to provide some general functions in the Simpact simulation (e.g. to keep track of relationships someone is in, or to keep track of children). Man and Woman classes are further specializations for properties which are only relevant to a specific gender (e.g. pregnancy or circumcision).
- SimpactEvent: This is a small wrapper class around PopulationEvent, and will redefine constuctors and some access functions to work with the Person class instead of the PersonBase class (to reduce the amount of type casting in event code).
- SimpactPopulation: this is a class derived from Population and is needed to create the initial people in the population (with varying properties) and to schedule an initial set of events.
To know how to use this population based algorithm, it can be useful to understand the way it works. The figure below illustrates how everything is organized. In essence, a population is just a collection of people and each person stores a list of events that are relevant to him.
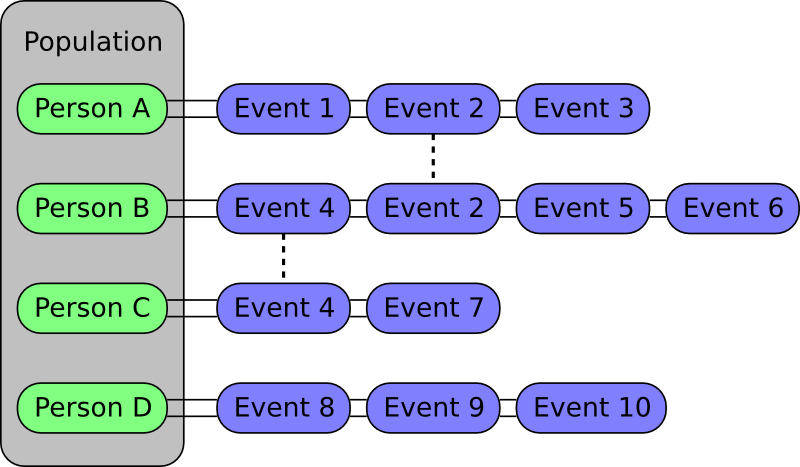
When you construct a new SimpactEvent based instance, you need to specify the persons involved in this event, and the event gets stored in these persons' lists. As the figure shows, it is very well possible that a single event appears in the lists of different people: for example a relationship formation event would involve two persons and would therefore be present in two lists. To be able to have global events, events that in principle don't affect people that are known in advance, a 'dummy' person is introduced. This 'dummy' person, neither labelled as a 'Man' nor as a 'Woman', only has such global events in its event list. By definition, these events will not be present in any other person's list. Note that this implies that PopulationEvent::getNumberOfPersons will also return 1 for global events.
When an event fires, the algorithm assumes that the persons which have the event in their lists are affected and that their events will require a recalculation of the fire times. In case other people are affected as well (who you don't know beforehand), this can be specified using the functions PopulationEvent::isEveryoneAffected or PopulationEvent::markOtherAffectedPeople. If such additional people are specified as well, those people's event fire times will be recalculated as well. Using PopulationEvent::areGlobalEventsAffected you can indicate that the fire times of global events should be recalculated.
Before recalculating an event fire time, it is checked if the event is still relevant. If one of the persons specified during the event creation has died, the event is deemed useless and will be discarded. In case it's possible that an event becomes useless because of some other criteria, the PopulationEvent::isUseless function should be reimplemented to inform the algorithm about this. But note that this is only called before recalculating an event fire time, which in turn is only done for people affected by the event.
Each person keeps track of which event in his list will fire first. To know which event in the entire simulation will fire first, the algorithm then just needs to check the first event times for all the people.
'Other affected persons' vs scheduling new events
Sometimes you have the choice between two approaches upon firing a certain event:
- Perform some action immediately, and if this involves other people than the ones specified when the event was created, these people should be accessible using the PopulationEvent::markOtherAffectedPeople function.
- Alternatively, you can schedule events that should take place (nearly) immediately, each event affecting one of the other people and having the 'fire' code for that event take appropriate action.
What choice is best will vary on the situation. As an example, suppose that in a simulation involving relationships, there's a 'mortality' event which causes a person to die. In this case, when such a mortality event fires, we'd also need to make sure that all relationships that the deceased person is in, are dissolved. But we cannot schedule new dissolution events for this: we cannot in general schedule events that involve a person who has already died, since that person is no longer present in the population. In this case, there's really no choice and method 1 must be used.
Working with the code
As you will see below, the CMake build system is used to generate configuration files (a makefile, a Visual Studio project file, ...) to actually build your programs. Since such files are overwritten when you run CMake, and running CMake is done automatically when one of the CMakeLists.txt files has been changed (these files contain a description of how the programs should be built), you should never ever directly modify one of those generated files**. For example, do not add source file names to the resulting Visual Studio project file. Instead, adjust the build configuration by modifying the CMakelists.txt files, as is explained below.
Directory structure
Described from the viewpoint of the top level directory of the code archive, the following things are relevant for building an application using the Simpact Cyan code:
- CMakeLists.txt:
to be able to work on different operating systems and to be able to use different development environments, the CMake build system is used. By pointing the CMake configuration utility to this top level directoy, it will start its configuration procedure by reading this file, which in turn performs some general tasks - cmake:
contains some helper code for the CMake build system - src:
this subdirectory contains the actual source code.- CMakeLists.txt:
another file that's part of the CMake configuration. This one will just point CMake to some additional directories for creating the main program and for creating test programs. - lib:
this subdirectory contains code for the mNRM, which is not specific for the Simpact Cyan case but could be reused for other simulations as well.- mnrm:
this directory contains the basis of the mNRM algorithm: the State class and an EventBase class. The straightforward algorithm from SimpleState is also in this directory. - core:
contains the population-based implementation of the mNRM, providing the classes Population, PersonBase and PopulationEvent. - util:
some utilities to read from a CSV file, to create an abstraction of a population age distribution, ... - errut:
a small utility to store error messages in a class.
- mnrm:
- program:
the code for the main simpact program, also containing a CMakeLists.txt file which specifies the source (.cpp) and header (.h) files to use. - tests:
the code for some test programs- test_mort:
directory containing a small test which creates a population of men and women and only schedules a mortality event for each person. Also contains a CMakeLists.txt file to let the build system know which files to use. - test1:
directory for a simple test with only debut, formation, dissolution and mortality events. Also contains a CMakeLists.txt file to let the build system know which files to use.
- test_mort:
- CMakeLists.txt:
CMake configuration
The top-level CMakeLists.txt (the first one in the list above), looks as follows:
This is not a file that should be modified. Basically it just makes sure that extra routines are available from SimpactMacros.cmake, then simpact_setup() is called to make sure that the routines from SimpactMacros.cmake are ready to be used later on, and finally the build system is told to continue from the CMakeLists.txt file that resides in the src subdirectory.
That file does not contain much either, it just tells CMake where to look for the build instructions of some programs:
In tests/test_mort for example, you'll find a set of source and header files, and also another CMakeLists.txt file which tells the build system what actually needs to be done:
The 'set' line just defines a variable named SOURCES_TEST to contain a number of filenames. The 'include_directories' line makes sure that when building the program, the compiler will also look in this directory for header files. The last line, with 'add_simpact_executable' is where all the magic happens. This causes the build system to define four executables with different settings: both in 'debug' mode and in 'release' mode (different compiler settings), and both using the very basic mNRM version (based on the SimpleState class) and the more optimized, population based version (based on the Population class).
When using a 'makefile' for building (in Linux for example), specifying the prefix 'testmort' in add_simpact_executable will cause four executables to be created:
- testmort-basic-debug: uses the algorithm from SimpleState, compiled with debug information
- testmort-basic: used the algorithm from SimpleState, but compiled with better compiler settings
- testmort-opt-debug: uses the algorithm from Population, compiled with debug information
- testmort-opt: uses the algorithm from Population, but compiled with better compiler settings
Here, the 'testmort-opt' should have the best performance, but it is always good to check from time to time that (for the same seed of the random number generator) the four versions of the executables generate exactly the same output. Different versions can use a different underlying algoritm and the debug versions perform lots of extra checks which do not occur in the other versions, but all should produce the same output for the same seed. Usually, you'll want a random seed to be chosen, but to check that all program versions are compatible, the random seed can be overridden by setting the environment variable MNRM_DEBUG_SEED to the value of the seed that you want to use.
If CMake generates project files for Visual Studio, the executables will be placed in 'Debug' and 'Release' subdirectories and will just be named 'testmort-basic' en 'testmort-opt' in each directory. In this case, the 'testmort-opt' version from the 'Release' subdirectory should perform best.
Specifying ${SOURCES_TEST} in that last line just substitutes the contents of that variable. The file could also just look like this:
So if you want to add another population-based simulation, you should create a directory for the source files below the src directory and add a line to the CMakeLists.txt file in that src directory. For example, if we were going to create a new program called 'mynewprogram', we'd create a directory with this name and add a line to the CMakeLists.txt file to make it look as follows:
In that directory we'd then add some source and header files, and we'd create a new CMakeLists.txt file that could look as follows:
Note that all executables are placed in the same directory, so make sure the names used by all the programs (including your new program) differ! (the things that must differ are the names used as the first parameter of add_simpact_executable, e.g. mynewprogram and test_mort).
Adding some code
Let's continue with the 'mynewprogram' example. In the CMakeLists.txt file, we've specified that a number of source files will need to be compiled, so we need to make sure that they exist. Apart from those files, we'll also be creating a number of header files.
In the mNRM engine provided by the Population class, a very general PersonBase class is used, which doesn't provide much functionality. To be able to add our own functions without having to modify the engine from the Population class, a number of subclasses will be defined. They won't have much use for this simple example, but they are a good place to start for a more advanced implementation. In a header file called person.h, the following code will be placed:
In this file, we're defining our own class called Person which can contain operations needed for either gender. The constructor is 'protected' so that no Person instances will be created directly; instead, a derived class (Man or Woman) must be used. As you can see, neither of these classes contain meaningful functionality, but they can be a good place to start. The implementation of these classes is in person.cpp and looks as follows:
The only thing that these implementations do, is make sure that the constructor of the base class is called correctly. The dateOfBirth parameters is always passed on unmodified, while the classes Man and Woman pass the correct gender specification on to the base class.
In the PopulationEvent class, a member function PopulationEvent::getPerson is present which returns a person that was mentioned at construction time. This function returns instances of the PersonBase type, which will in fact be either Man or Woman, classes derived from PersonBase (by deriving from Person). We'll be needing to interpret these classes as a Person more often than as a PersonBase, so to avoid type-casting in our event code, we'll define a new SimpactEvent class in which the getPerson member function already performs the cast. This class is specified in simpactevent.h where all the code resides (i.e. there is no corresponding cpp file).
This class simply forwards the constructor to the PopulationEvent constructor and provides a getPerson function that calls the PopulationEvent::getPerson function and type-casts the result. This way, the compiler will know that we're certain the PersonBase instance can safely be interpreted as a Person instance.
For this simple test program, we'll define an event called EventTest, which inherits from SimpactEvent and which uses the same implementations as EventBase::getNewInternalTimeDifference, EventBase::calculateInternalTimeInterval and EventBase::solveForRealTimeInterval. These default implementations use a simple exponential probability distribution to pick internal time intervals from, and use the trivial mapping from internal time to real world time, i.e. internal time intervals equal real world time intervals. We will reimplement the PopulationEvent::getDescription function for logging purposes and we'll provide an implementation for the fire function (which won't contain any actual code though):
The event refers to one person, so it will only be in that person's event queue. The implementation for this class is in eventtest.cpp and looks as follows:
The Population class contains the implementation of the mNRM algorithm that we're going to use, but it does not contain any code to initialize the population, to schedule initial events or to log what's happening. For these reasons we're defining our own SimpactPopulation class, derived from Population, specified in simpactpopulation.h:
This header file defines an init function which will create an initial number of men and women, and which will schedule an initial set of events. It also reimplements State::onAboutToFire, which is called right before an event gets executed using its fire function. In that function we'll just log which event is taking place. We're also overriding the getAllPeople, getMen and getWomen functions, which just call the corresponding function from Population and tell the compiler it's safe to interpret them as an array of general Person instances, an array of Man instances or an array of Woman instances. The implementation of this class will be stored in simpactpopulation.cpp** and looks as follows:
In the init function, we check if some criteria are met, returning false to indicate that something went wrong and storing an error description to let the caller of the function know what precisely is the matter. This setErrorString function is actually defined in errut::ErrorBase, which is a parent class of State. Then, a number of Man and Woman instances are created with age 10 at the start of the simulation (so their birth date is -10), and are introduced into the population using Population::addNewPerson. In the scheduleInitialEvents member function, we'll just schedule a single test event for everyone in the population where each event is introduced into the mNRM algorithm by calling Population::onNewEvent. In the onAboutToFire function (re-implemented from State::onAboutToFire) we'll just print out the description of the event that's being fired.
To finish this small test program, we still need to implement a main function, the starting point of our application. In this example, the file containing this function is called main.cpp and contains the following code:
In this main function, we specify the random number generator (of type GslRandomNumberGenerator) which is to be used in the entire simulation. This random number generator is passed on to the simulation algorithm using the SimpactPopulation constructor, and must exist the entire time the simulation is being used. Next, the population's init function is called, specifying that 1000 men and women are to be introduced. The simulation is then run using the run member function, specifying a maximum simulation time that's so large that there's really no limit, and specifying a negative value for maxEvents to indicate that the number of events is not limited. When this function returns, the contents of tMax and of maxEvents will have been altered to contain the last simulation time and the number of events executed.
Running the program
After compiling everything (we're assuming a Linux build), you should find four executables:
- mynewprogram-opt
- mynewprogram-opt-debug
- mynewprogram-basic
- mynewprogram-basic-debug
With a random seed, the output of mynewprogram-opt could start with the following for example:
In which case it would end with these lines:
The lines starting with '#' at the beginning of the output are generated by the algorithm used and provide some information which could be useful later on, for example the seed used for the random number generator (could be useful to check if the same output is generated by one of the other three programs), if the 'advanced' or 'basic' version of the algorithm was used and if the 'Debug' or 'Release' version is used. As explained above, for a Linux build the '-opt' suffix means that the advanced algorithm is being used with better (release) compiler settings, and this is also reported in the output here.
This simulation just runs until no more events are present in the system, which is reported as an error. If we were to make a histogram of the times events take place, we'd obtain the following distribution:
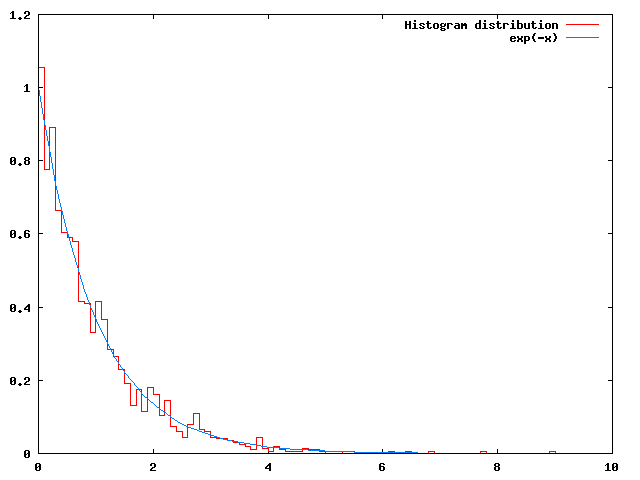
Because we're using a constant hazard 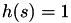 in the EventTest class, we're just seeing the distribution used for the internal event times: an exponential distribution.
in the EventTest class, we're just seeing the distribution used for the internal event times: an exponential distribution.
The Simpact Cyan program
The full Simpact Cyan program can be found in the src/program subdirectory. This program contains several events that can take place, the Person class is more elaborate to keep track of relationships, number of children, HIV infection status etc, but the overall structure of the program is the same as the simple example explained above. Some documentation about using the resulting program can be found here.
Since this program is still under development, finished documentation of all the classes and functions used is not available currently. Below you'll find some general information that may be helpful though.
More often than not, you'll need access to the person that was specified in the constructor of a SimpactEvent class. As in the example above, this is done by specifying Person instances, which can be accessed using the getPerson member function. This getPerson function of the SimpactEvent class overrides the implementation from PopulationEvent::getPerson, and makes sure the person is returned as a Person instance (instead of a PersonBase instance).
Sometimes you'll need access to functions that are present in a Man or Woman subclass, so if you know what gender the person is, you can call the functions MAN or WOMAN to reinterpret a Person instance as either a Man or a Woman instance. In debug mode, a check is done in these functions to make sure that the gender setting matches the type you're trying to convert to, but for performance reasons this check is not done in release mode. An example of such a function call can be found in the fire function of the birth event, where we need to reset the 'pregnant' flag of the mother (which does not exist for a Man instance):
When an event fires, your own re-implementation of EventBase::fire is called. Using an argument to this function, the state is passed as a State object. In our own implementation, we've derived a class called SimpactPopulation from Population, which in turn derives from State. Similar to the MAN and WOMAN functions, there's a function called SIMPACTPOPULATION that you can use to reinterpret such a State pointer as a SimpactPopulation reference. Make sure that if the source State object has a const specifier, the destination reference also has one or the compiler will complain. For example, the fire code of the mortality event looks like this:
Because the source pState does not have a const specifier, the target population variable doesn't need one either. However, in the getNewInternalTimeDifference function, which does use a const State pointer, the destination reference also needs to have this const:
In this Simpact Cyan program, you'll always derive an event from the SimpactEvent class, which is almost identical to the code shown above. You can reimplement the functions EventBase::getNewInternalTimeDifference, EventBase::calculateInternalTimeInterval and EventBase::solveForRealTimeInterval to determine which distribution you're using to generate new internal time intervals and to calculate the mapping between such internal time intervals and real world event fire times.
By default, the getNewInternalTimeDifference function chooses a time interval from the simple exponential distribution 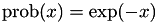 , analogous to the description in the mNRM article. So if that's ok for your event, you don't have to provide an implementation for that function and you can just let the base class handle this. To map an internal time interval onto a real world time and vice versa, you then only need to implement the
, analogous to the description in the mNRM article. So if that's ok for your event, you don't have to provide an implementation for that function and you can just let the base class handle this. To map an internal time interval onto a real world time and vice versa, you then only need to implement the solveForRealTimeInterval and calculateInternalTimeInterval functions.
On the other end of the spectrum you could also easily create an event that fires at a specific real world time using these functions. You'll then need to reimplement getNewInternalTimeDifference so that it returns the real world time interval until the event fires. And that's all you'll need to do: in the default implementations of calculateInternalTimeInterval and solveForRealTimeInterval internal time intervals already equal real world time intervals, so you won't need to add those functions to your class anymore.
To cancel the future execution of an event, you can reimplement the PopulationEvent::isUseless function. Before this function is called, a check has already been done to see if one of the persons specified in the constructor (of the SimpactEvent derived class) has died. If so, the event will be cancelled and no further check is done. Otherwise, the PopulationEvent::isUseless function is called and if this returns true, the event is cancelled as well. Note that this function is only called for events that would require a recalculation of their mapping from internal time to real world time, which are the events queued in the event lists of persons relevant to the event that has just been fired.
As an example of this, consider the following code in the transmission event, which is used to transfer HIV infection from an infected person onto an uninfected one:
When looking at any part of the code, you'll see many 'assert' function calls. This is a check that is executed when compiling the program in 'debug' mode, but is skipped when compiling the program in 'release' mode. Using such checks is strongly encouraged: if at some point you believe a condition should always hold, add an 'assert' call to verify this. While this can still make your program go wrong or even crash in release mode, being able to pinpoint such a failed check in debug mode can greatly speed up the search for the mistake. Since it is much easier to add such lines when you're creating the code than when you're looking for a bug that you haven't been able to pinpoint yet, I strongly recommend adding such 'assert' checks while you're adding a function**. Such assertions are very helpful in preventing and tracking down conceptual mistakes, which are the worst kind since they don't cause an immediate crash of your program but do generate results that are incorrect.
 1.8.6
1.8.6